| Submeter | Todas submissőes | Melhores | Voltar |
DUENDE - Duende Perdido |
Gugo, o duende, ficou preso em uma caverna e precisa sair o mais rapidamente possível. A caverna é formada por salões interligados por túneis, na forma de uma grade retangular, com N linhas e M colunas. Alguns dos salões da caverna têm paredes de cristal. Duendes, como todos sabem, não gostam de ficar em ambientes com qualquer tipo de cristal, pois seus organismos entram em ressonância com a estrutura de cristais, e em casos extremos os duendes podem até mesmo explodir. Compreensivelmente, Gugo não quer entrar em nenhum salão com parede de cristal.
A figura abaixo mostra uma caverna com quatro linhas e cinco colunas de salões; os salões cinza têm paredes de cristal. A posição inicial de Gugo é indicada com um caractere ‘*’.
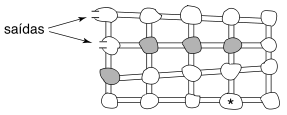
Tarefa
Você deve escrever um programa que, dadas a configuração da caverna e a posição inicial de Gugo dentro da caverna, calcule qual o número mínimo de salões pelos quais o duende deve passar antes de sair da caverna (não contando o salão em que o duende está inicialmente), mas contando o salão que tem saída para o exterior).
Entrada
A caverna será modelada como uma matriz de duas dimensões, cujos elementos representam os salões. Um salão que não tem parede de cristal e que tem saída para o exterior da caverna é representado pelo valor 0; um salão que não tem parede de cristal e não tem saída para o exterior é representado pelo valor 1; um salão que tem parede de cristal é representado pelo valor 2; e o salão em que o duende está inicialmente (que não tem saída para o exterior e nem paredes de cristal) é representado pelo valor 3. A figura abaixo mostra a representação da caverna apresentada acima.
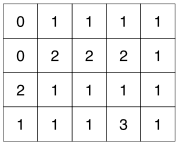
A primeira linha da entrada contém dois números inteiros N e M que indicam respectivamente o número de linhas (1 <= N <= 10) e o número de colunas (1 <= M <= 10) da representação da caverna. Cada uma das N linhas seguintes contém M números inteiros Ci, descrevendo os salões da caverna e a posição inicial do duende (0 <= Ci <= 3). Você pode supor que sempre há um trajeto que leva Gugo à saída da caverna.
Saída
Seu programa deve produzir uma unica linha na saída, contendo um número inteiro representando a quantidade mínima de salões pelos quais Gugo deve passar antes de conseguir sair da caverna (não contando o salão em que ele está inicialmente, mas contando o salão que tem saída para o exterior).
Exemplo 1Entrada: 4 5 0 1 1 1 1 0 2 2 2 1 2 1 1 1 1 1 1 1 3 1 Saída: 8 |
Exemplo 2Entrada: 1 10 2 0 1 1 3 1 1 1 0 1 Saída: 3 |
Restrições
1 <= N <= 10
1 <= M <= 10
0 <= Ci <= 3
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2008-04-02 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP JS-RHINO PERL6 PY_NBC SCALA TCL |
| Origem: | Olimpíada Brasileira de Informática 2005 -- Programaçăo Nível 1 |
hide comments
|
2017-04-12 21:17:36
Funciona nos testes mas recebendo WA. Alguma dica de corner case? |
|
|
2013-06-20 21:19:59 Sergillam Oliveira []
kkkkkkkk |
|
|
2012-06-10 03:12:37 Paula Moraes Leardine
Até a parte se montar a matriz e randomizar as posiçőes, blz. ofroy está sendo achar a saida e fazer a contagem... |
|
|
2012-05-25 13:16:51 Igor Borges [UNIFEI]
Ele é um duende; năo pode usar mágica? |
|
|
2011-09-09 00:09:47 thiagojobson [UERN]
Algoritmo do path finding :D |
