| Submit | All submissions | Best solutions | Back to list |
ADAHOSE - Ada and Hose |
As you might already know, Ada the Ladybug is a farmer. She owns a square field. There is a hose wrapped around each 1×1 sub-field. All hoses are additionally combined into a bigger hose everywhere where they touch (so the water can arbitrarily flow between both of them [or even all four of them]). Each hose has its own flow-per-time attribute.
There is a big well (an infinite source of water) above the field and a big sprinkler under the field. Additionally very big hoses (for our case we can consider them infinitely big) are lead from well to top of the field and from bottom to the sprinkler. Your quest is simple: Calculate the maximal total flow-per-time which goes from well to sprinkler.
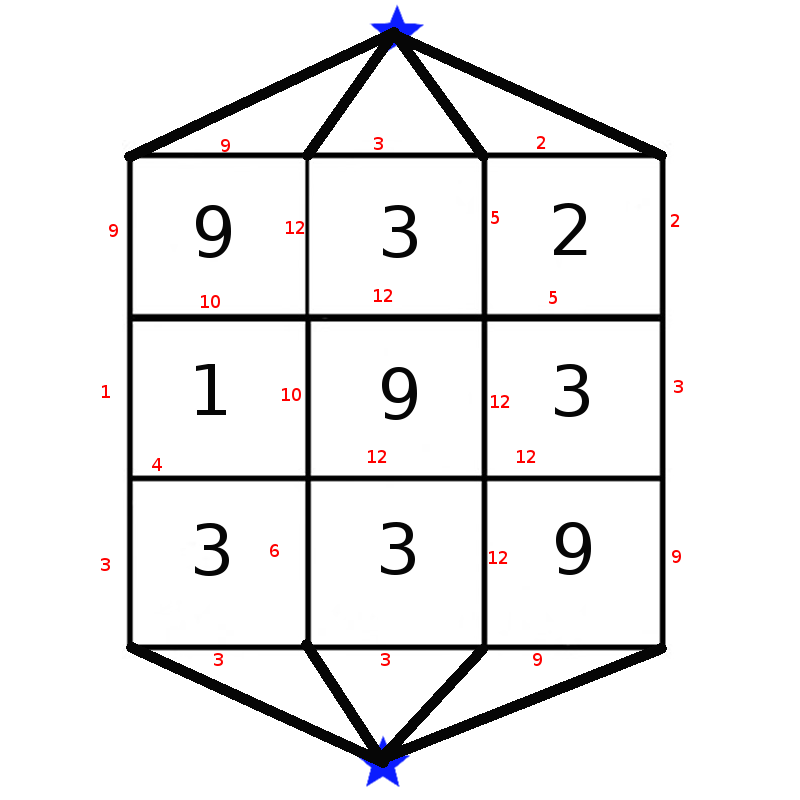
Input
The first line of input contains an integer 1 ≤ N ≤ 1000, the size of field.
The next N lines contains N integers 0 ≤ Aij ≤ 1000, the size of each hose wrapped around.
Output
Output the maximal flow-per-time achievable.
Example Input
3 9 3 2 1 9 3 3 3 9
Example Output
26
Example Input 1
4 2 0 0 2 0 2 2 0 2 0 0 2 0 2 2 0
Example Output 1
8
Example Input 2
8 2 2 0 1 2 1 5 1 5 1 3 7 1 6 3 1 3 8 5 3 6 6 8 8 2 9 6 6 8 2 3 0 5 4 3 9 7 1 0 4 2 5 1 5 2 5 6 5 5 3 8 3 9 8 1 1 8 9 0 8 2 3 1 9
Example Output 2
28
| Added by: | Morass |
| Date: | 2017-10-16 |
| Time limit: | 2s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
hide comments


 RSS
RSS