| Submit | All submissions | Best solutions | Back to list |
ANARC08A - Tobo or not Tobo |
The game of Tobo is played on a plastic board designed into a 3X3 grid with cells numbered from 1 to 9 as shown in figure (a). The grid has four dials (labeled 'A' to 'D' in the figure.) Each dial can be rotated in 90 degrees increment in either direction. Rotating a dial causes the four cells currently adjacent to it to rotate along. For example, figure (b) shows the Tobo after rotating dial 'A' once in a clockwise direction. Figure (c) shows the Tobo in figure (b) after rotating dial 'D' once in a counterclockwise direction.
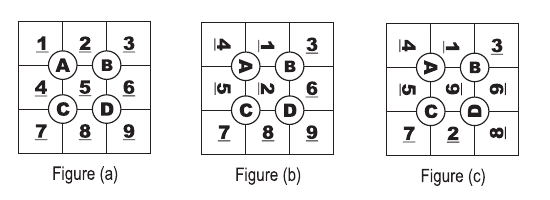
Kids love to challenge each other playing the Tobo. Starting with the arrangement shown in figure (a), (which we'll call the standard arrangement,) one kid would randomly rotate the dials, X number of times, in order to shuffle the board. Another kid then tries to bring the board back to its standard arrangement, taking no more than X rotations to do so. The less rotations are needed to restore it, the better. This is where you see a business opportunity. You would like to sell these kids a program to advise them on the minimum number of steps needed to bring a Tobo back to its standard arrangement.
Input
Your program will be tested on one or more test cases. Each test case is specified on a line by itself. Each line is made of 10 decimal digits. Let's call the first digit Y . The remaining 9 digits are non-zeros and describe the current arrangement of the Tobo in a row-major top-down, left-to-right ordering. The first sample case corresponds to figure (c).
The last line of the input file is a sequence of 10 zeros.
Output
For each test case, print the result using the following format:
k. R
where k is the test case number (starting at 1,) is a single space, and R is the minimum number of rotations needed to bring the Tobo back to its standard arrangement. If this can't be done in Y dials or less, then R = -1.
Example
Input:
3413569728
1165432789
0000000000
Output:
1. 2
2. -1
| Added by: | Ahmed Aly |
| Date: | 2009-07-02 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | ANARC 2008 |
hide comments
|
2019-06-12 14:27:05
meet in the middle...try to reach to "123456789" from the start in half of y if you reach then OK else try to reach to start from "123456789" in the remaining of y (y - y / 2) if you reach OK else we try to make a link in the middle ..How to do that...well , when you search from start keep the distance and sum in an unordered_map and do the same thing when you search from end("123456789") ..the rest is standard :) |
|
|
2018-10-18 21:51:51
pre processing |
|
|
2014-07-22 19:59:07 Archit Jain
enjoyed solving it time limit is very strict ..:( Last edit: 2014-07-22 21:34:30 |
|
|
2009-07-08 17:23:46 majid
Time limit is very very very strict :( . We can't solve it with java. Plz increase time limit ... |
|
|
2009-07-04 21:27:51 Seckin Can Sahin
The problem description is wrong and misleading. "If this can't be done in Y dials or less, then R = -1." means, we can use at most 2 dims if Y=2, not all ABCD but one of {AB,AC,AD,BC,BD,CD,A,B,C,D}. I looked at the official problem set and it is the same there, really weird. It should be "If this can't be done in Y rotations or less, then R = -1." Last edit: 2009-07-05 12:15:18 |
|
|
2009-07-03 04:25:26 Eigenray
Apparently we don't care about the orientations of the numbers even though the diagram makes a point of showing them. That was a bit confusing. That is, the group of arrangements has index 2 in the wreath product of Z_2 by S_9: G = H x| S_9, where H < F_2^9 is the irreducible component of dimension 8. So the kernel of the projection G -> S_9 has order 2^8, meaning the arrangement isn't uniquely determined by the permutation as given in the input. So I guess we are actually working in the quotient G/H = S_9. |


 RSS
RSS