| Submit | All submissions | Best solutions | Back to list |
COVER - K-path cover |
Problem
K-path cover of a directed graph is a set of exactly k of its edges chosen in such way that every two of them have different start vertices and every two of them have different end vertices. Assuming that for each vertex we know its cost we can define cost of the edge as a sum of costs of its start and end. We can also define cost of a k-path cover as a sum of costs of its edges. Your task is to find cheapest k-path cover for given directed graph with known costs of the vertices.
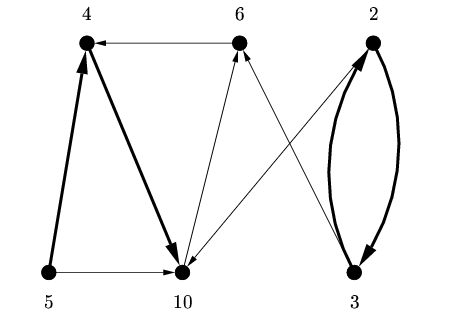
A graph and its cheapest 4-path cover.
Input
First line of input contains number of test cases c (1<=c<=20). Each test case begins with k, number of vertices n and number of edges m (1<=k<=100, 1<=n<=10000, 0<=m<=1000000). Next n lines contain costs of the vertices, each of them is an integer from [-100000,100000]. Then m lines describing edges follow, each of them containing exactly two numbers representing its start and end vertices. Vertices are numbered from 1 to n.
Output
For each test case output cost of the cheapest k-path cover. When given graph has no k-path cover output NONE.
Example
Input: 1 4 6 9 5 4 6 10 2 3 1 2 1 4 2 4 3 2 4 3 5 4 6 3 5 6 6 5 Output: 33
| Added by: | gawry |
| Date: | 2005-08-08 |
| Time limit: | 1.205s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS PERL6 VB.NET |
| Resource: | ONTAK 05 |


 RSS
RSS