| Submit | All submissions | Best solutions | Back to list |
FLBRKLIN - Flat broken lines |
We have a cartesian coordinate system drawn on a sheet of paper. Let us consider broken lines that can be drawn with a single pencil stroke from the left to the right side of the sheet. We also require that for each segment of the line the angle between the straight line containing this segment and the OX axis belongs to [-45°, 45°] range. A broken line fulfilling above conditions is called a flat broken line. Suppose we are given n distinct points with integer coordinates. What is the minimal number of flat broken lines that should be drawn in order to cover all the points (a point is covered by a line if it belongs to this line)?
Example
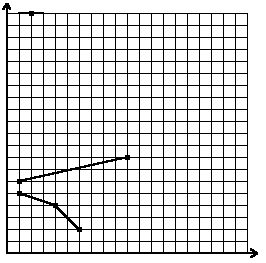
For 6 points whose coordinates are (1,6), (10,8), (1,5), (2,20), (4,4), (6,2) the minimal number of flat broken lines covering them is 3.
Task
Write a program that for each test case:
- reads the number of points and their coordinates;
- computes the minimal number of flat broken lines that should be drawn to cover all the points;
- outputs the result.
Input
The number of test cases t is in the first line of input, then t test cases follow separated by an empty line.
In the first line of a test case there is one positive integer n, not greater than 30000, which denotes the number of points. In the following n lines there are coordinates of points. Each line contains two integers x, y separated by a single space, 0 <= x <= 30000, 0 <= y <= 30000. The numbers in the i-th line are the coordinates of the i-th point.
Output
For each test case you should output one line with the minimal number of flat broken lines that should be drawn to cover all the points.
Example
Sample input: 1 6 1 6 10 8 1 5 2 20 4 4 6 2 Sample output: 3
| Added by: | Michał Czuczman |
| Date: | 2004-08-10 |
| Time limit: | 5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | 5th Polish Olympiad in Informatics, stage 3 (Grzegorz Jakacki, Krzysztof Sobusiak) |


 RSS
RSS