| Submit | All submissions | Best solutions | Back to list |
GASOLINE - Pizza Store and Gasoline |
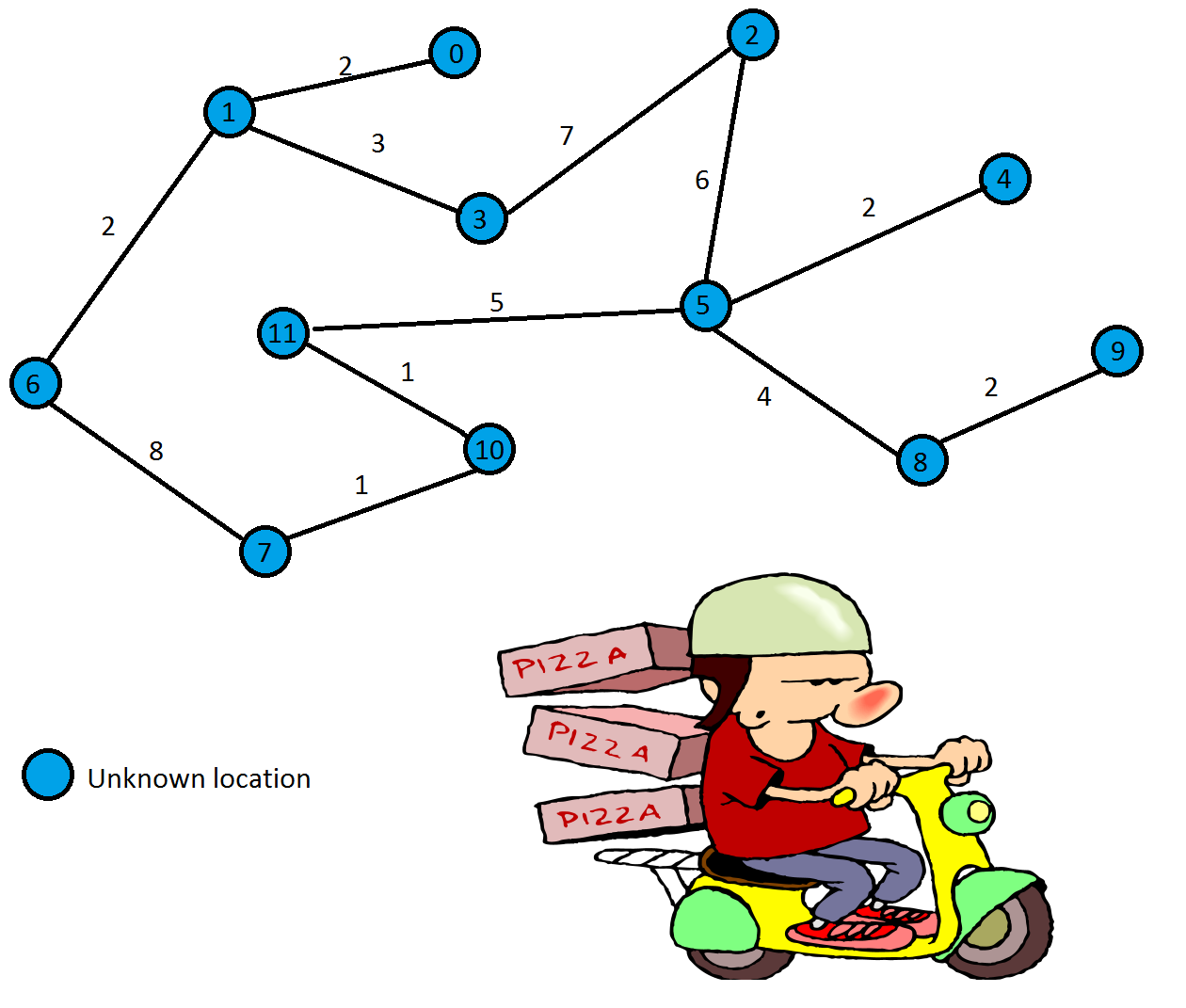
A pizza delivery company owner gives you a map which contains n locations and m connecting roads. (vertices and edges). The locations are numbered from 0 to n-1. You are also given the length of each road. To travel, one unit distance, the motor bike needs 1 unit of gasoline. The company owner neither has the delivery location of the pizza nor the location of the stores.
Now the company owner asks you "What is the minimum amount of Gasoline needed in a motor bike to deliver one pizza order?". Can you answer him?
Input
The first line consists of an integer t, the number of test cases. For each test case, the first line consists of two integers n and m denoting the number of locations and roads respectively. The next m lines consists of 3 integers a, b and l denoting the road that connects two locations a and b with length l.
Output
For each test case, find the minimum amount of gasoline needed in order to deliver one pizza order. If it is impossible to deliver the order, print -1.
Constraints
1 ≤ t ≤ 50
1 ≤ n ≤ 500
0 ≤ m ≤ 500
a ≠ b
1 ≤ l ≤ 100
Sample
Input: 1 12 12 0 1 2 1 3 3 1 6 2 6 7 8 7 10 1 10 11 1 11 5 5 2 3 7 5 2 6 4 5 2 8 5 4 8 9 2 Output: 24
Explanation
For the given test case, 24 units of gasoline is sufficient to deliver a pizza regardless of the store location and delivery location.
Note
There can be more than one road between a pair of locations.
| Added by: | cegprakash |
| Date: | 2016-10-22 |
| Time limit: | 20s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: BF GOSU |
hide comments
|
2017-01-01 03:59:28 rainy jain
@cegprakash I'm getting WA. Please check submission id:18492671 |


 RSS
RSS