| Submit | All submissions | Best solutions | Back to list |
GRIDSUM3 - 2x2 Subgrid Sum Problem (generalized) |
This problem is a higher constraints and generalized version of KWACIK (Polish) and GRIDSUM2.
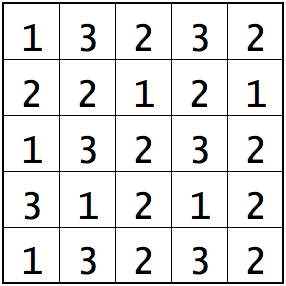
You are given a kxk grid. You can place an integer m (a ≤ m ≤ b) in each cell.
How many ways are there to place integers in the cells such that the sum of each 2x2 subgrid is n ?
Since the answer might be very large, output it modulo 479001600 (= 12!).
Input
The first line contains an integer T (1 ≤ T ≤ 104), the number of test cases.
On each of the next T lines, you are given four integers k, a, b and n.
(2 ≤ k ≤ 5, 0 ≤ a ≤ b ≤ 5 * 108, 0 ≤ n ≤ 2 * 109)
Output
For each test case, output a single line containing the number of ways to place integers modulo 479001600 (= 12!).
Example
Input:
4 2 1 2 4 3 1 2 5 4 1 3 6 5 1 3 8
Output:
1 8 74 1383
Explanation
There are 8 ways to place integers for k=3, a=1, b=2 and n=5.
2 1 2 : 2 1 2 : 2 1 1 : 1 2 1 : 1 2 1 : 1 1 2 : 1 1 1 : 1 1 1 1 1 1 : 1 1 1 : 1 1 2 : 1 1 1 : 1 1 1 : 2 1 1 : 2 1 2 : 1 2 1 2 1 2 : 1 2 1 : 2 1 1 : 2 1 2 : 1 2 1 : 1 1 2 : 1 1 1 : 1 1 1
Credit & Special thanks
- Bartek - the original problem author
- Mitch Schwartz
| Added by: | Min_25 |
| Date: | 2014-10-17 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | KWACIK |


 RSS
RSS