| Submit | All submissions | Best solutions | Back to list |
IMPORT1 - The Importance |
Given an undirected weighted graph {V,E}. Your task to calculate the importance of each node.
The importance of a node v (I(v)) can be defined as follow:
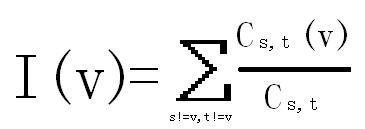
Cs,t is the number of different shortest paths from s to t, Cs,t(v) is the number of different shortest paths from s to t through v.
Input
Multiple test cases, the number of them is given in the very first line.
For each test case:
The first line contains two space-separated integers n (n ≤ 100) and m (m ≤ 4500), the number of nodes in the graph and the number of edges in the graph. The nodes are numbered from 1 to n. m lines follow, each contains 3 integers a, b, c, 1 ≤ a, b ≤ n, 1 ≤ c ≤ 1000, a ≠ b, which denotes that there is an undirected edge between node a and node b weighted c. You may assume that there is at most one edge between any pair of nodes, and the number of shortest paths between any pair of nodes is at least 1 and at most 1010.
Output
For each test case:
Your Output should contains n lines, each contains one single real number, with 3 decimal places after radix point. The number in the ith line denotes the importance of the ith node.
Example
Input: 1 4 4 1 2 1 2 3 1 3 4 1 4 1 1 Output: 1.000 1.000 1.000 1.000
| Added by: | Fudan University Problem Setters |
| Date: | 2007-08-05 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: C99 ERL JS-RHINO |
| Resource: | Chinese National Olympiad in Informatics 2007,Day 1; Translated by Blue Mary |


 RSS
RSS