| Submit | All submissions | Best solutions | Back to list |
JC15F - Colorful Beads |
Colorful Beads

Yay, today is colorful day! why? because there are so many colorful beads on the table. Satria want to make a necklace using all that available beads, in order to make the necklace most valuable, Satria arrange the beads using magic secret formula. Gunawan secretly want to know Satria's secret formula, so he try all possible beads combination until the beads become most valuable, at first he easily found the most valuable beads combination for small number of beads, but he can't derive general formula, he keeps trying, and tying, and trying... Never give up!
Someday, Tjandra meet Gunawan and suggest him to not continuing his bruteforce action because the number of possible combinations are too many. Gunawan doesn't believe that and ask Tjandra to show him number of possible combinations.
Gunawan said: "If I have this N beads how many combinations are there?"
Tjandra replied: "It's N facorial combinations"
Gunawan replied: "But that's not always true some of my beads has more than one color, so if I swap beads with same color doesn't change tha necklace value"
Tjandra replied: "Okay, tell me the details of your beads"
Gunawan replied: "My beads has M distinct colors, it has K1 beads of color 1, K2 beads of color 2, ... , KM beads of color M"
Tjandra replied: "It will have F(K1+K2+...+KM)/(F(K1)*F(K2)*...*F(KM)) combinations where F(N) means N factorial"
(5 minutes later)
Gunawan said: "Hey, your formula is not true, I tried it with 2 green beads and 2 blue beads, your formula showed F(2+2)/(F(2)*F(2)) = 24/(2*2) = 6 combinations, but actually it has only 2 combinations"
Tjandra confidently replied: "I'm good at math, I'm sure my formula is correct"
Gunawan replied: "I made these two different necklace: {1:{g,g,b,b},2:{g,b,g,b}} [g=green beads, b=blue beads] can you make the third necklace that is different than both of these?"
Tjandra replied: "That's easy, here is the third necklace: {b,g,b,g} "
Gunawan replied after rotating that necklace: "Look, your neclace become equal to my second necklace: {b,g,b,g} -> {g,b,g,b}"
Tjandra replied: "Oops, I forgot about necklace rotation, you'really smart bruteforcer, why you don't believe me that number of combination is too many even though it's a little bit smaller than my calculation"
Gunawan replied: "A little bit? do you think 6 and 2 is little difference?"
Tjandra replied: "huh -_- I can show you that the exact number of distinct combinations, but unfortunately the formula become too complex and I don't bring a computer, is there any computer here?"
Gunawan replied: "No, I'm also don't have a computer"
Now Tjandra call you using his old phone for help, because he know that now you're sitting in front of your computer. Can you help them?
Input
The first line there is an integer K denoting number of distinct beads colors.
On the second line there are K integers, Ki is number of beads with i-th color.
Output
Print single integer that is the number of distinct color combination. Since this number is very large as Tjandra predict, output it modulo 109+7.
Constraint
1 ≤ K ≤ 1000
1 ≤ Ki ≤ 1000
Sample 1
Input
1
1000
Output
1
Sample 2
Input
2
2 2
Output
2
Sample 3
Input
3
1 1 1
Output
2
Sample 4
Input
4
2 3 4 5
Output
180180
Sample 5
Input
5
1 2 3 4 5
Output
2522520
Sample 3 Explanation
On sample 3 there are 3 distinct color of beads, there is 1 bead for each color.
Let's assume those 3 distinct color are red, green, and blue,
here are 2 possible necklace, all other beads combination can be rotated to obtain one of thoose necklace below.
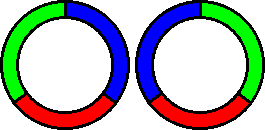
Note that if we can flip the necklace, both necklace are equal, but in this problem, we assume the front side of necklace is different than the back side, so both necklace above are considered different.
| Added by: | Tjandra Satria Gunawan |
| Date: | 2016-01-18 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 GOSU JS-MONKEY |
| Resource: | Own Problem, used in Jolly Challenge #15 |


 RSS
RSS