| Submit | All submissions | Best solutions | Back to list |
JPIX - Pixel Shuffle |

Shuffling the pixels in a bitmap image sometimes yields random looking images. However, by repeating the shuffling enough times, one finally recovers the original images. This should be no surprise, since "shuffling" means applying a one-to-one mapping (or permutation) over the cells of the image, which come in finite number.
Your program should read a number n , and a series of elementary transformations that define a "shuffling" 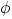 of n * n images. Then, your program should compute the minimal number m (m > 0) , such that m applications of
of n * n images. Then, your program should compute the minimal number m (m > 0) , such that m applications of 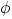 always yield the original n * n image.
always yield the original n * n image.
For instance if 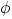 is counter-clockwise 90o rotation then m = 4.
is counter-clockwise 90o rotation then m = 4.

Input
Test cases are given one after another, and a single 0 denotes the end of the input. For each test case:
Input is made of two lines, the first line is number n (2 <= n <= 210 , n even). The number n is the size of images, one image is represented internally by a n * n pixel matrix (aji) , where i is the row number and j is the column number. The pixel at the upper left corner is at row 0 and column 0.
The second line is a non-empty list of at most 32 words, separated by spaces. Valid words are the keywords id, rot, sym, bhsym, bvsym, div and mix, or a keyword followed by -. Each keyword key designates an elementary transform (as defined by Figure 1), and key- designates the inverse of transform key. For instance, rot- is the inverse of counter-clockwise 90o rotation, that is clockwise 90o rotation. Finally, the list k1, k2, ..., kp designates the compound transform 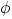 = k1ok2o ... okp . For instance, "bvsym rot-" is the transform that first performs clockwise 90o rotation and then vertical symmetry on the lower half of the image.
= k1ok2o ... okp . For instance, "bvsym rot-" is the transform that first performs clockwise 90o rotation and then vertical symmetry on the lower half of the image.

Figure 1: Transformations of image (aji) into image (bji)

Output
For each test case:
Your program should output a single line whose contents is the minimal number m (m > 0) such that 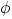 is the identity. You may assume that, for all test input, you have m < 231.
is the identity. You may assume that, for all test input, you have m < 231.
Example
Input: 256 rot- div rot div 256 bvsym div mix 0 Output: 8 63457
| Added by: | Fudan University Problem Setters |
| Date: | 2007-12-01 |
| Time limit: | 1.5s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: C99 ERL JS-RHINO |
| Resource: | ACM Central European Programming Contest, Budapest 2005 |
hide comments
|
2018-07-12 12:40:03
Shouldn't the sequence in the second test case be reversed? |
|
|
2015-11-23 20:21:35
finally!!! after 4WA's got AC!!!!!!! |
|
|
2015-03-25 14:55:16 (Tjandra Satria Gunawan)(曾毅昆)
I don't know what the intended complexity for this problem, at first I got TLE using ~2KB O((number of keyword)*(n^2)) algo, but AC with same complexity after applying ultra heavy constant optimization, code is 4.5 × longer than unoptimized one (~9KB). I hope at least O(n^2 + (number of keyword)*n*log^2(n)) algo exist (I don't know yet), otherwise I don't like this problem where advanced constant optimization needed. I spent full days to do crazy optimization near low level. btw, It's better if number of test case mentioned in problem description so solver (including me) can prepare good complexity algo/strategy before coding especially if the code will be long (>2KB). |
|
|
2009-12-26 00:18:28 Brian Bi
Tip: Cache efficiency. |


 RSS
RSS