| Submit | All submissions | Best solutions | Back to list |
MAZE - The Long and Narrow Maze |
Consider a maze consisting of 3 rows of n square blocks each. The passageways in every block match one of three possible patterns, numbered 0 (empty), 1 (straight) and 2 (bent), as depicted below.
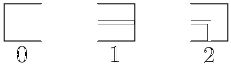
Your task is to determine whether it is possible to create a passage in a given maze, with an entrance at the left end and an outlet at the right end of the maze, only by rotating some of the squares of the maze by a multiple of 90 degrees.
Input
The input begins with the integer t, the number of test cases. Then t test cases follow.
Each test case begins with a line containing a single integer n - the number of squares in one row of the maze (1 ≤ n ≤ 200000). The next n lines contain three integers each, denoting the types of blocks in consecutive columns of the maze. A column description is of the form a b c (0 ≤ a, b, c ≤ 2), where a represents the type of the block in the first row, b - in the second row and c - in the third row.
Output
For each test case output the word yes if it is possible to rotate the squares so as to form a connection between the left and right edge, and the word no in the opposite case.
Example
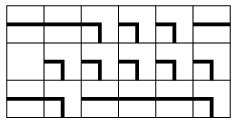
Input: 1 6 1 0 1 1 2 2 2 2 1 2 2 1 2 2 1 1 2 2 Output: yes
Indeed, the sample input corresponds to the following maze:
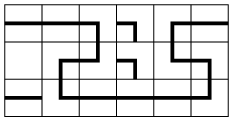
for which there exists a correct solution to the problem:
| Added by: | adrian |
| Date: | 2004-07-19 |
| Time limit: | 10s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All |
| Resource: | VI Polish Collegiate Team Programming Contest (AMPPZ), 2001 |
hide comments
|
2017-06-03 12:54:36
Getting WA...Even though I've considered every test case I can think of... |


 RSS
RSS