| Submit | All submissions | Best solutions | Back to list |
MRECT1 - Point on the side of the rectangle |
| English | Vietnamese |
The government is planing to build a walkway for tourists in the middle of an oak forest. The forest
can be represented as plane with N special lattice points representing oaks.
rectangle intersect any oak lattice points, such oaks need to be axed down. Oaks inside the rectangle
not represent problems and need not be cut do
Ljubo is the state secretary of Forestry and an passionate nature lover, so he ordered the secretary of
Tourism to provide him with a list of P possible rectangle walkways that are attractive enough to draw
Cho N điểm và P hình chữ nhật trên mặt phẳng tọa độ. Tính xem với mỗi hình chữ nhật có bao nhiêu
điểm nằm ở trên cạnh của nó trong P điểm đã cho.
Input
Dòng đầu ghi số điểm N (1 ≤ N ≤ 300 000), N dòng tiếp theo mỗi dòng ghi 2 số X, Y (1 ≤ X, Y ≤ 10^9) . Không có hai điểm nào trùng nhau.
Dòng tiếp theo ghi số P, (1 ≤ P ≤ 100 000), số hình chữ nhật.
P dòng tiếp theo, mỗi dòng ghi 4 số X1, Y1, X2 , Y2 (1 ≤ X1 < X2 ≤ 10^9, 1 ≤ Y1 < Y2 ≤ 10^9)
là tọa độ góc trái dưới (X1, Y1) và góc phải trên (X2, Y2) của từng hình chữ nhật.
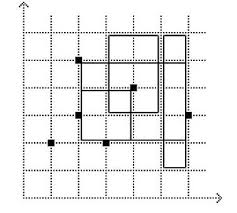
Output
Ghi ra P số nguyên, mỗi số trên 1 dòng, là số điểm nằm trên cạnh của từng hình chữ nhật.
Sample
input
6
1 2
3 2
2 3
2 5
4 4
6 3
4
2 2 4 4
2 2 6 5
3 3 5 6
5 1 6 6
output
3
4
0
1
in tourists.
Ljubo plans to select the walkway that needs the smallest amount of oak trees to be cut down. Since we
also like trees, would you be so kind and write a program that will determine the number of oaks that
will be cut down for each walkway. Remember only the oaks intersecting the sides of the rectangle
need to be cut.
| Added by: | psetter |
| Date: | 2010-05-24 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS OBJC PERL6 SQLITE VB.NET |
| Resource: | COI 2010 |


 RSS
RSS