| Submit | All submissions | Best solutions | Back to list |
NSTEPS - Number Steps |
Starting from point (0,0) on a plane, we have written all non-negative integers 0, 1, 2, ... as shown in the figure. For example, 1, 2, and 3 has been written at points (1,1), (2,0), and (3, 1) respectively and this pattern has continued.
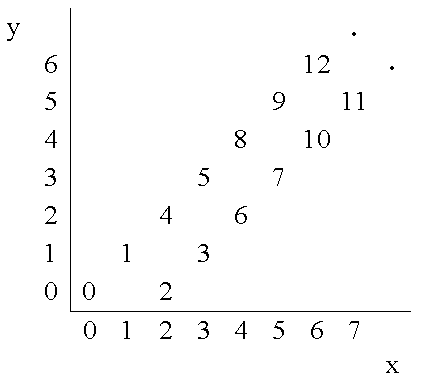
You are to write a program that reads the coordinates of a point (x, y), and writes the number (if any) that has been written at that point. (x, y) coordinates in the input are in the range 0...10000.
Input
The first line of the input is N, the number of test cases for this problem. In each of the N following lines, there is x, and y representing the coordinates (x, y) of a point.
Output
For each point in the input, write the number written at that point or write No Number if there is none.
Example
Input: 3 4 2 6 6 3 4 Output: 6 12 No Number
| Added by: | Camilo Andrés Varela León |
| Date: | 2006-11-25 |
| Time limit: | 1.159s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | Asia - Tehran 2000 |
hide comments
|
||||||||||||||
|
2021-03-16 07:33:28
whats wrong with this <snip> [NG]: It's wrong not to read the rules in the footer. Last edit: 2021-03-16 15:53:24 |
||||||||||||||
|
2021-03-04 11:28:08
My WAs are equal to number of ACs people got in comment sections: Hints : See even & odd patterns separately, get equation on paper. It'll take time. There is space between No Number and both N are capitol Try this test case 7 7 gives 13 as answer Don't think about slope equation or some geometric equation, its not that thing. Just a normal relation Last edit: 2021-03-04 11:28:41 |
||||||||||||||
|
2020-11-24 22:26:22
@anurag_mishra. no you dont |
||||||||||||||
|
2020-11-24 15:15:46
you have take all inputs then print awnser otherwise WA |
||||||||||||||
|
2020-08-13 18:30:49
try to search for a pattern |
||||||||||||||
|
2020-08-10 08:09:45
i got the logic to find the solution but made one mistake i.e make sure given x,y lie on lines x=y or x-y=2 |
||||||||||||||
|
2020-06-02 08:20:48
sdfsd |
||||||||||||||
|
2020-05-08 18:29:47
i am getting sigabrt error. please help |
||||||||||||||
|
2020-02-29 06:36:52
Just look for even and odd pattern :) |
||||||||||||||
|
2020-01-21 09:58:05
just observe the pattern and you are good to go! There is a uniform difference everywhere. |
||||||||||||||


 RSS
RSS