| Submit | All submissions | Best solutions | Back to list |
SAMER08A - Almost Shortest Path |
Finding the shortest path that goes from a starting point to a destination point given a set of points and route lengths connecting them is an already well known problem, and it's even part of our daily lives, as shortest path programs are widely available nowadays.
Most people usually like very much these applications as they make their lives easier. Well, maybe not that much easier.
Now that almost everyone can have access to GPS navigation devices able to calculate shortest paths, most routes that form the shortest path are getting slower because of heavy traffic. As most people try to follow the same path, it's not worth it anymore to follow these directions.
With this in his mind, your boss asks you to develop a new application that only he will have access to, thus saving him time whenever he has a meeting or any urgent event. He asks you that the program must answer not the shortest path, but the almost shortest path. He defines the almost shortest path as the shortest path that goes from a starting point to a destination point such that no route between two consecutive points belongs to any shortest path from the starting point to the destination.
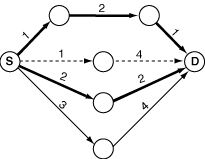
For example, suppose the figure below represents the map given, with circles representing location points, and lines representing direct, one-way routes with lengths indicated. The starting point is marked as S and the destination point is marked as D. The bold lines belong to a shortest path (in this case there are two shortest paths, each with total length 4). Thus, the almost shortest path would be the one indicated by dashed lines (total length 5), as no route between two consecutive points belongs to any shortest path. Notice that there could exist more than one possible answer, for instance if the route with length 3 had length 1. There could exist no possible answer as well.
Input
The input contains several test cases. The first line of a test case contains two integers N (2 ≤ N ≤ 500) and M (1 ≤ M ≤ 104), separated by a single space, indicating respectively the number of points in the map and the number of existing one-way routes connecting two points directly. Each point is identified by an integer between 0 and N -1. The second line contains two integers S and D, separated by a single space, indicating respectively the starting and the destination points (S ≠ D; 0 ≤ S, D < N).
Each one of the following M lines contains three integers U, V and P (U ≠ V; 0 ≤ U, V < N; 1 ≤ P ≤ 103), separated by single spaces, indicating the existence of a one-way route from U to V with distance P. There is at most one route from a given point U to a given point V, but notice that the existence of a route from U to V does not imply there is a route from V to U, and, if such road exists, it can have a different length. The end of input is indicated by a line containing only two zeros separated by a single space.
Output
For each test case in the input, your program must print a single line, containing -1 if it is not possible to match the requirements, or an integer representing the length of the almost shortest path found.
Example
Input: 7 9 0 6 0 1 1 0 2 1 0 3 2 0 4 3 1 5 2 2 6 4 3 6 2 4 6 4 5 6 1 4 6 0 2 0 1 1 1 2 1 1 3 1 3 2 1 2 0 3 3 0 2 6 8 0 1 0 1 1 0 2 2 0 3 3 2 5 3 3 4 2 4 1 1 5 1 1 3 0 1 0 0 Output: 5 -1 6
| Added by: | Diego Satoba |
| Date: | 2008-11-23 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | C CPP JAVA PAS-GPC PAS-FPC |
| Resource: | South American Regional Contests 2008 |
hide comments
|
||||||||
|
2017-04-08 12:36:40
fastio required |
||||||||
|
2017-01-02 17:23:35
Find and store all shortest paths by running Dijkstra’s algorithm only once. Delete all edges of all shortest paths from adjacency list. Run Dijkstra’s algorithm again after deletion In Dijkstra’s algorithm, during relaxation ancestor (or parent) of a vertex in shortest path(SP) can be stored and kept updating in an array or any similar container i.e. index represents a vertex and value at index represents it’s ancestor in SP. When multiple ancestor of a vertex yield paths of same length, then we can store all of them in array of containers like: vector, set etc. Then that array of containers will become an adjacency list for shortest paths(SPs) for all (ancestor-successor) vertexes in any SP. If path finding algorithm like DFS or BFS is applied to that array of containers from destination vertex to source then all possible SPs can be stored. |
||||||||
|
2016-12-22 18:34:56
Excellent problem! Must do! |
||||||||
|
2016-10-03 19:14:33
Nice problem! |
||||||||
|
2016-10-03 18:33:34
@sunny .. see carefully first shortest path is 0->1->2->3 of len 30 second shortest is 0->1->4->5->6->3 of len 30 nd then comes the remaining i.e 0->7->8->3 of len 200 |
||||||||
|
2016-09-25 07:11:58 Sunny
@root25.. i am referring to the test case posted by baqir00..... the original shortest path is 0->1->2->3 with length equal to 30 and the next shortest path should be 0->4->5->6->3 with length 31...Why 200? |
||||||||
|
2016-09-13 17:04:41
My code works fine on my local computer but gives segmentation fault on SPOJ. Please help! <snip> Last edit: 2023-05-15 20:25:39 |
||||||||
|
2016-08-20 16:30:56
@baqir00.. The Answer is indeed 200..I've Cross checked it. Make sure you have Covered possible combinations for the Input. Hope this Helps. |
||||||||
|
2016-06-29 19:27:31
Can anyone tell me the output of 9 11 0 3 0 1 10 0 7 80 0 4 22 1 4 11 1 2 10 2 3 10 4 5 5 5 6 2 6 3 2 7 8 100 8 3 20 0 0 Acc. to me it should be 31, which is what my program outputs, but according to spoj, its 200. Am I missing something? |
||||||||
|
2016-06-16 13:18:29 ADITYA PRAKASH
easy but must do |
||||||||


 RSS
RSS