| Submit | All submissions | Best solutions | Back to list |
TRICOUNT - Counting Triangles |
We define the LEVEL of a triangle as in the following illustrative image:
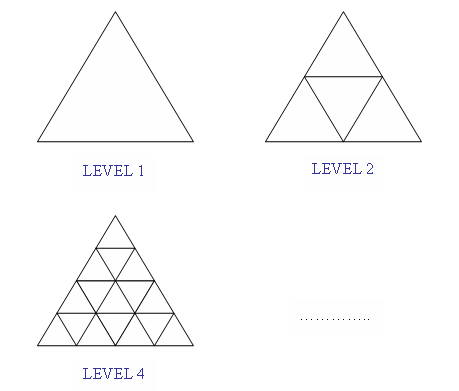
Task: Your task is very easy. All you have to do is to count all triangles in the biggest one (Level N).
Input
The first line of the input contains an integer T (T ≤ 10000) - the number of test cases and T lines follow. Each line contains an integer N (1 ≤ N ≤ 106) which is the level of the triangle in that test case.
Output
For each test case, you should write a seperate line: the number of triangles in the biggest one (Level N). (All answers will fit within the range of a 64-bit integer)
Example
Input:
3
1
2
3
Output:
1
5
13
Source limit is 500 bytes.
| Added by: | nha.duong |
| Date: | 2007-08-05 |
| Time limit: | 1s |
| Source limit: | 500B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 ERL JS-RHINO NODEJS OBJC PERL6 SQLITE VB.NET |
| Resource: | Trần Huy Hưng |
hide comments
|
||||||||||||||
|
2018-09-27 16:14:29
Java Users use Buffered Reader Instead of Scanner |
||||||||||||||
|
2018-08-30 16:10:59
cout<<pow(2,n+1)-3<<endl; |
||||||||||||||
|
2018-08-24 12:36:25
for the intuition of the formula: https://www.youtube.com/watch?v=9EU3FlKj-3M Last edit: 2018-08-24 12:36:46 |
||||||||||||||
|
2018-06-30 19:29:36
What is the pattern here? missing 3rd level figure makes it hard to understand it. Can anybody explain the pattern? |
||||||||||||||
|
2018-06-22 17:53:46
Is using the formula necessary? I wrote the program using functions separately for upwards and downwards(odd-even), and it's working fine.. But the file size is exceeding 500B, in C++. How to fix this? Last edit: 2018-08-11 17:11:23 |
||||||||||||||
|
2018-06-21 07:12:30
For those who are getting TLE in java, use Bufferreader instead of scanner ;) |
||||||||||||||
|
2018-06-03 00:18:03
shubham31 ...you missed those inverted triangles add them and get AC :) |
||||||||||||||
|
2018-06-01 17:16:24
I am using this recurrence relation but it is giving TLE f(n) = (2*n - 1) + (n*(n-1))/2 + f(n-1); f(1) = 1 |
||||||||||||||
|
2018-05-29 15:14:03
note there is different formula for even and odd values of N |
||||||||||||||
|
2018-05-25 13:45:02
Method apart from formula: observe the pattern of the number of triangles facing upward and downward. Store upward and downward triangles in 2 arrays and add them to get the answer. |
||||||||||||||


 RSS
RSS