| Submit | All submissions | Best solutions | Back to list |
TTOP - Tree Topology |
Given a rooted tree, a permutation of its nodes is valid if the following holds: for each pair of nodes a and b, if a is an ancestor of b, then a appears before b in the permutation. Let P(t) be the number of valid permutations for a tree t.
Given an integer N, you can construct all the possible trees of N nodes, numbered from 1 to N, rooted at 1. I'd like to know what's the sum of P(t) for all t that can be constructed for the given N.
We consider two trees equal iff each node in the second tree has the same parent as it does in the first one.
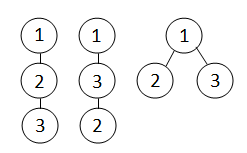
The picture shows all the possible trees for N = 3.
Input
A single integer N (1 ≤ N ≤ 1000000).
Output
A single integer representing the solution modulo 1000000007.
Example
Input:
3
Output:
4
Explanation: If you take a look at the picture, you'll see that the first two trees have one valid permutation each, and the third tree has two, namely { 1, 2, 3 } and { 1, 3, 2 }. The total is, of course, 4.
| Added by: | gustav |
| Date: | 2010-12-04 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ASM64 |
| Resource: | own problem |
hide comments
|
2023-01-22 15:07:04
if anyone struggling answer for 4 is 36 |
|
|
2011-08-22 15:28:51 m@j!n {Amit Gupta}
if the input is 4 and 5 then what will be the output for these values answer: Judging by the correct submissions, the problem is well defined, so you may try finding a solution on paper... Also, I'd suggest finding a solution without figuring out patterns. Last edit: 2010-12-10 16:09:31 |


 RSS
RSS