| Submit | All submissions | Best solutions | Back to list |
WM06 - Soccer Choreography |
Mr. Bitmann, the coach of the national soccer team of Bitland, is a perfectionist. He taught his players optimal tactics and improved their endurance and shape. So they qualified for the soccer woldcup this year. Due to his perfectionism the coach attaches importance not only to the performance in the game but also before the game. So he told the team captain in what formation the team should assemble before the national anthem is played. Since each of the 11 team members has a unique number between 1 and 11 on his shirt, he can represent the formation as a permutation of numbers.
Before the first game the coach told the captain that the team should line up in increasing order (picture (d)). But some players forgot the ordering and the orientation of the formation like in picture (a). Only player 1 has the right orientation. The coach went nearly mad when he saw this desaster! How could he solve the problem?
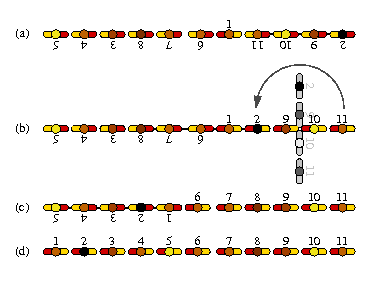
"Hmmm... I'll let my players dance!". A great idea! He took his notebook and started to create a choreography which leads to his expected formation. Due to the fact that no one of the players took dancing lessons he restricts his dance to one basic move: One player or more players who stand side by side can turn 180 degrees around the center of the move. Picture (b) contains an example: The players
-11 -10 -9 -2
(we mark players which stand in the wrong direction with a minus) can do one move to
2 9 10 11
As perfect as he is he calculated a dance with a minimum number of moves. It works perfectly and now he's planning to do dancing performances with teams with more than 11 members. So he needs your help to find optimal dancing moves...
Input
Each testcase starts with the number of team members n (0<=n< 2200). The next lines represent the formation at the beginning and the expected formation at the end of the choreography.
Output
For each testcase output m, the minimal number of moves which are necessary to reach the expected formation. The next m+1 lines should represent one possible scenario of moves.
Example
Input: 11 -5 -4 -3 -8 -7 -6 1 -11 -10 -9 -2 1 2 3 4 5 6 7 8 9 10 11 11 1 2 3 -4 -5 -6 -7 -8 -9 10 11 11 9 8 7 6 5 4 3 2 10 1 0 Output: 3 Steps -5 -4 -3 -8 -7 -6 +1 -11 -10 -9 -2 -5 -4 -3 -8 -7 -6 +1 +2 +9 +10 +11 -5 -4 -3 -2 -1 +6 +7 +8 +9 +10 +11 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 5 Steps +1 +2 +3 -4 -5 -6 -7 -8 -9 +10 +11 +1 +2 -3 -4 -5 -6 -7 -8 -9 +10 +11 +1 -2 -3 -4 -5 -6 -7 -8 -9 +10 +11 +1 -2 -3 -4 -5 -6 -7 -8 -9 -11 -10 +11 +9 +8 +7 +6 +5 +4 +3 +2 -1 -10 +11 +9 +8 +7 +6 +5 +4 +3 +2 +10 +1
| Added by: | Simon |
| Date: | 2006-05-11 |
| Time limit: | 8s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | ADA95 ASM32 BASH BF C CSHARP CPP C99 CLPS LISP sbcl LISP clisp D FORTRAN HASK ICON ICK JAVA LUA NEM NICE OCAML PAS-GPC PAS-FPC PERL PHP PIKE PRLG-swi PYTHON RUBY SCM guile SCM qobi ST WHITESPACE |
hide comments
|
||||||
|
2009-09-30 03:19:34 .:: dEE ::.
Can a person be that center of the move? i.e. can { -5 -4 -3 } be rotated to { 3 4 5 } ? |
||||||
|
2009-03-28 21:42:45 Johannes Laire
Hmm, ok. I just can't see any better way to get an optimal solution than a tree search, but that doesn't work because the search space is... huge. (Finding a move sequence that just works but is not necessarily optimal would be fairly trivial, of course.) I'll come back to this problem later and try to find the O(n^2) algorithm, thanks for confirming that it's possible. Last edit: 2009-03-28 21:42:45 |
||||||
|
2009-03-28 07:26:03 [Trichromatic] XilinX
I don't think you are right, because there exists an algorithm with O(n^2) time complexity to this problem. Edit: Obviously a program with time complexity higher than O(n^2) can not work. SPOJ has a few problems of this kind, like FTOUR, FTOUR2. Last edit: 2009-03-28 07:26:03 |
||||||
|
2009-03-28 19:51:34 Johannes Laire
The upper bound of 2200 combined with 1s-2s time limit is ridiculous. I have a working program, but without any knowledge of what the test cases are like, it's practically impossible to optimize it enough. Last edit: 2009-03-28 19:51:34 |
||||||


 RSS
RSS