| Submit | All submissions | Best solutions | Back to list |
WONKA1 - Wonkas Oompa-Impa Dilemma |
Willy Wonka, the amazing Chocolatier, appears to have a serious predicament at hand. You see, the worker population of his large factory, which consists of 100% Oompa Loompas, is facing a massive decline. This started off because of the fatal accidents in the testing of new Wonka products, but the decline has grown ever since then as old age was slowly factored into the equation. Because Oompa Loompas are as of yet a completely male tribe, they cannot simply reproduce amongst themselves to make up for their dying comrades.
So Willy Wonka has travelled out into the uncharted terrain of LoompaLand once more in an attempt to find wives for the Oompa Loompas. This trip is not fruitless, since he soon comes across the Impa Limpas, a tribe of civilized females in search of husbands.
Problem solved, you say?? Well, not exactly. Since these are civilized women who have embraced the power of logic and wisdom, they will not give consent to marry savages. To test the Oompa Loompas' intellectual capacity, they have set up a task for them. Standing at an angle (possibly perpendicular) to a completely flat field in the dead center of LoompaLand, the Impa Limpas have set up 2 totem poles facing each other. One belongs to the Impa Limpas while the other belongs to the Oompa Loompas.

The objective of this task, given the ratio of descent of each totem pole (this ratio is how many degrees the totem pole falls per second), is to determine how many seconds apart the totem poles should be pushed so that they end up with their tops touching and all motion stopped. Willy Wonka knows that the angle at which a totem pole initially stands at in relation to the field will not determine the direction it falls in, only the direction of the push will do this (which should normally be towards the other totem pole). No matter what the situation, you can assume that all motion is stopped once the tops of the poles meet; keep in mind that gravity has nothing to do with this problem.
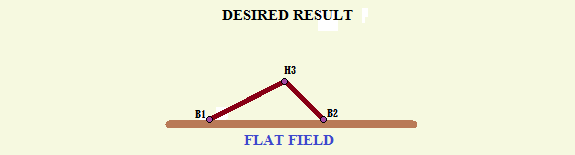
The Impa Limpas are gracious with this task and have provided a 2D representation (done with a Cartesian Plane) of their totem poles' set-up to the Oompa Loompas, but they're not THAT gracious... they have rotated the actual diagram in relation to some point by some degrees, so the field may appear to be elevated. Since Oompa Loompas are, in fact, mostly savages, Willy Wonka has no faith in their problem solving capabilities. He attempted to solve this task himself, but seeing as how he dropped out of school early to go into the chocolate making business, his math skills aren't that great. So he has turned to his last hope: you (the boy (or girl...he forgets which) he inspired to become a programmer). Willy Wonka will give you 6 pieces on information: H1 and H2 (the points of the tops of the totem poles), B1 and B2 (the points of the bottom of the totem poles), and A1 and A2 (the ratio of decent of each totem pole). You are to solve this task for your childhood hero at all costs! Don't let Willy down.
Input
The first line contains an integer T (with 1 ≤ T ≤ 10000), specifying the number of test cases that will follow.
Each of the following T lines contain 4 (x, y) coordinates giving 4 seperate points on the Cartesian Plane: H1, B1, H2, and B2 (-50000 ≤ x, y ≤ 50000), in that order and 2 real numbers A1 and A2 (0 < A1, A2 ≤ 90), giving each totem pole's degree of descent per second after initial push.
Output
Output is a single real number S (rounded off to the nearest 1000th), where S is the absolute value of the difference in the number of seconds that each totem pole has in the air after it has been pushed before all motion has been stopped by the Oompa Loompas' and the Impa Limpas' totem poles meeting. In the case that this requirement is never met (say, for instance, that the totem poles come crashing down onto the field without their tops ever meeting) then the program should output "-1".
Example
Input: 3 0 5 0 0 6 5 6 0 1 1 -1 6 -4 5 -1 3 -2 1 0.5 0.25 4 -1 3 -1 4 -5 3 -5 12 10.6 Output: 0.000 61.087 -1
Input Explanation
Case 1:- H1 Coordinates: (0, 5)
- B1 Coordinates: (0, 0)
- H2 Coordinates: (6, 5)
- B2 Coordinates: (6, 0)
- A1 Ratio: 1 degree drop per second (clockwise, in this case)
- A2 Ratio: 1 degree drop per second (counter-clockwise, in this case)
- H1 Coordinates: (-1, 6)
- B1 Coordinates: (-4, 5)
- H2 Coordinates: (-1, 3)
- B2 Coordinates: (-2, 1)
- A1 Ratio: 0.5 degree drop per second
- A2 Ratio: 0.25 degree drop per second
- H1 Coordinates: (4, -1)
- B1 Coordinates: (3, -1)
- H2 Coordinates: (4, -5)
- B2 Coordinates: (3, -5)
- A1 Ratio: 12 degree drop per second
- A2 Ratio: 10.6 degree drop per second
Output Explanation
Case 1:It takes both totem poles the exact same amount of time to reach the point where their tops hit each other. The difference as expressed through S is thus 0.
Case 2:For the tops of the totem poles to meet, one totem pole must be pushed approximately 61.087 seconds before the other.
Case 3:The tops of the totem poles will never meet, so you must print "-1" as shown.
Hint
Pencil and paper is the way to go!
| Added by: | Ammar Qadri |
| Date: | 2010-06-29 |
| Time limit: | 0.104s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: NODEJS OBJC PERL6 SQLITE VB.NET |
| Resource: | An Original (By Ammar Qadri) |
hide comments
|
2010-07-21 13:31:20 Darth Vadar
Hey all the test cases and some cases of my own are working perfectly but still its coming WA.BTW for precision, if the ans is 0, do we need to print 0.000 or just 0 will suffice |
|
|
2010-07-07 01:22:29 Lewin Gan
The poles aren't necessarily initially parallel. The picture is a little misleading Last edit: 2011-03-02 12:19:41 |
|
|
2010-07-06 11:23:50 Anuj Arora
I have a doubt, both poles should be parallel to each other in initial setup as they are perpendicular to the flat field. But with respect to Case 2, they are not parallel. Any light on my doubt is highly appreciable. Thanks. |
|
|
2010-07-02 18:03:35 Ammar Qadri
Guys make sure that the language you use rounds in the conventional style. Please try to use math to solve this problem. If I see any cheap functions, your solution will be disqualified. And, just so that there is no fuss over the accuracy, I used (pi = 3.1415926535897932384626434). Last edit: 2010-06-30 18:00:54 |


 RSS
RSS