SPOJ Brasil

Você possui vários pedaços retangulares de papelão como o da Figura 1-(a) e deve fazer uma caixa com cada um deles. Para isso vai cortar quadrados nos cantos (Figura 1-(b)) e dobrar as laterais (Figura 1-(c)), formando uma caixa (aberta em cima).

(a) Papelão retangular

(b) Cantos cortados

(c) Caixa resultante

Figura 1: Formando uma caixa com papelão retangular

Os cantos cortados são quadrados do mesmo tamanho. A dúvida é: qual o tamanho dos lados desses cortes quadrados para que a caixa tenha o maior volume possível?

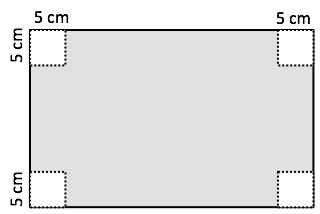
Por exemplo, com um pedaço de papelão de 25 x 40 cm (Figura 2-(a)), o ideal é cortar quadrados de 5 cm (Figura 2-(b)), e assim obterá uma caixa de volume 2250 cm^3 (Figura 2-(c)).

(a) Papelão 25 x 40 cm

(b) Cortes quadrados 5 x 5 cm

(c) Caixa de volume 2250 cm^3

Figura 2: Formando caixa de maior volume possível

Entrada

Cada linha da entrada contém dois inteiros A e B que são as dimensões, em cm, de um padaço de pepelão (10 ≤ A ≤ 500, 10 ≤ B ≤ 500). O fim da entrada é indicado por uma linha contendo dois zeros.

Saída

Para cada linha da entrada, escreva uma linha na saída, contendo dois valores: o tamanho do lado do quadrado que deve ser cortado para obter o volume máximo, e o valor do volume máximo assim obtido. Todo os valores devem ser escritos arredondados para 4 casas decimais.

Exemplos

Entrada:
25 40
300 300
100 80
0 0

Saída:
5.0000 2250.0000
50.0000 2000000.0000
14.7247 52513.8043