| Submeter | Todas submissőes | Melhores | Voltar |
FLOREST2 - Floresta |
O desmatamento é um dos maiores problemas enfrentados pelo Brasil hoje; estima-se que mais de 10 mil km² de vegetação sejam desflorestados todo ano. Além de destruir os habitats de várias espécies em risco de extinção, o desmatamento promove a emissão de gás carbônico, principal responsável pelo efeito estufa e pelo aquecimento global.
A Fundação de Conservação dos Carvalhos (FCC) tenta combater esta tendência, promovendo o reflorestamento das regiões desmatadas. Para isso, eles pretendem plantar carvalhos formando um quadriculado (um carvalho em cada vértice); no centro de cada quadrado formado por eles, a FCC também plantará um eucalipto. Para preservar a biodiversidade da área plantada, pelo menos uma árvore de cada espécie deve ser plantada durante o reflorestamento.
Por exemplo, se a FCC quiser plantar 23 árvores, ela poderá fazê-lo de duas maneiras: ou formando um retângulo 3 × 5 com os carvalhos, como na figura (a), ou formando um retângulo 2 × 8, como na figura (b).
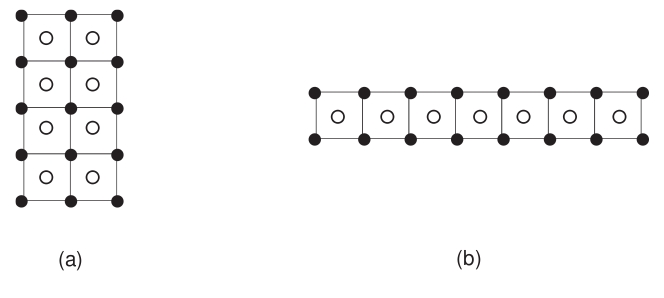
Considere que, para os propósitos deste problema, um retôngulo x × y é equivalente a um retângulo y × x.
Tarefa
Escreva um programa que, dado o número total de árvores que devem ser plantadas, de quantas maneiras diferentes elas podem ser dispostas.
Entrada
A única linha da entrada contém um único inteiro N, que indica o número total de árvores que devem ser plantadas (1 ≤ N ≤ 109) .
Saída
Seu programa deve imprimir uma única linha, contendo um único inteiro, indicando o número de arranjos distintos que podem ser feitos para o reflorestamento.
Exemplo
Entrada 23 Saída 2 Entrada 7 Saída 0 Entrada 53 Saída 3
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2011-04-28 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP PERL6 PY_NBC SCALA TCL |
| Origem: | OBI 2010 - fase 2 nível 2 |
