| Submeter | Todas submissőes | Melhores | Voltar |
MAGICO11 - Quadrado mágico |
Arnaldo e Bernardo são dois garotos que compartilham um peculiar gosto por curiosidades matemáticas. Nos últimos tempos, sua principal diversão tem sido investigar propriedades matemágicas de tabuleiros quadrados preenchidos com inteiros. Recentemente, durante uma aula de matemática, os dois desafiaram os outros alunos da classe a criar quadrados mágicos, que são quadrados preenchidos com números de 1 a N2, de tal forma que a soma dos N números em uma linha, coluna ou diagonal principal do quadrado tenham sempre o mesmo valor. A ordem de um quadrado mágico é o seu número de linhas, e o valor do quadrado mágico é o resultado da soma de uma linha. Um exemplo de quadrado mágico de ordem 3 e valor 15 é mostrado na figura abaixo:
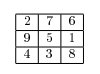
Para surpresa de Arnaldo e Bernardo, os outros alunos criaram um grande número de quadrados, alguns enormes, e alegaram que todos eram quadrados mágicos. Arnaldo e Bernardo agora precisam de sua ajuda, para verificar se os quadrados criados são realmente mágicos.
Você deve escrever um programa que, dado um quadrado, verifique se ele é realmente mágico.
Entrada
A primeira linha da entrada contém um único número inteiro N, indicando a ordem do quadrado (seu número de linhas). As N linhas seguintes descrevem o quadrado. Cada uma dessas linhas contém N números inteiros separados por um espaço em branco.
Saída
Seu programa deve imprimir uma única linha. Caso o quadrado seja mágico, a linha deve conter o valor do quadrado (ou seja, a soma de uma de suas linhas). Caso contrário, a linha deve conter o número 0.
Restrições
- 3 ≤ N ≤ 1000.
- 1 ≤ valor de cada célula ≤ 109.
Exemplos
Entrada 3 1 1 1 1 1 1 1 1 1 Saída 0 Entrada 4 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 Saída 34 Entrada 3 4 8 9 11 7 3 6 5 10 Saída 0
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2012-03-10 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP PERL6 PY_NBC SCALA TCL |
| Origem: | OBI 2011 - fase 2 nível 2 |
hide comments
|
2016-04-07 22:45:23 Elsio [UFABC]
Se as diagonais forem iguais, não precisa confirmar mais nada. (isso é uma falha kkk) |
|
|
2014-08-27 20:30:21 benevides
galera tem algo errado,copiei e colei o codigo da OBI(tinha testado o meu programa no corretor da OBIe fechado,so fiz isso pra conferir) e nem o codigo da OBI passou |
|
|
2013-09-17 03:03:20 Alexandre Henrique Afonso Campos
O caso 2 é o quadrado mágico de consta na Melencolia I (no ano 15 14) de Albrecht Dürer. Além das somas convencionais serem 34, cada quadrado 2x2 também soma e as quintas. Isso é só curiosidade. Năo influi no problema. |
|
|
2012-09-14 23:00:57 Stankevix [UFSCar]
Năo entendi como, contar ou saber se ele informou números repetidos.Tem que criar um novo contador para comparar? Last edit: 2012-09-17 20:51:55 |
|
|
2012-08-31 20:47:25 Ordan Santos
Last edit: 2013-02-17 20:17:11 |
|
|
2012-06-20 14:12:17 Paulo César[UFG]
Porque năo pode haver números repetidos. |
|
|
2012-05-28 19:32:43 Artur Freitas
Esse daí năo é mágico porque os quadrados devem ser preenchidos de 1 a N˛, sendo N o número de linhas. Last edit: 2012-05-28 19:33:36 |
|
|
2012-04-18 17:54:21 Jeferson Lesbão de Siqueira[UNITAU]
Estou com um codigo rodado O(N^2) no pior caso, e ainda tomo time limit-exceeded.. isso ta muito estranho. |
|
|
2012-04-14 05:44:01 Marcos Kawakami
Todos os números de 1 a N^2 devem ser usados exatamente uma vez. |
|
|
2012-04-11 18:59:39 Jeferson Lesbão de Siqueira[UNITAU]
por que o quadrado: 3 1 1 1 1 1 1 1 1 1 năo é magico ? |
