| Submeter | Todas submissőes | Melhores | Voltar |
MINHOCA2 - Campo de Minhocas |
Minhocas são muito importantes para a agricultura e como insumo para produção de ração animal. A Organização para Bioengenharia de Minhocas (OBM) é uma entidade não governamental que promove o aumento da produção, utilização e exportação de minhocas.
Uma das atividades promovidas pela OBM é a manutenção de uma fazenda experimental para pesquisa de novas tecnologias de criação de minhocas. Na fazenda, a área destinada às pesquisas é de formato retangular, dividida em células quadradas de mesmo tamanho. Em cada célula é criada apenas uma espécie de minhoca. As células são utilizadas para testar os efeitos, sobre a produção de minhocas, de variações de espécies de minhoca, de tipos de terra, de adubo, de umidade, etc. Os pesquisadores da OBM mantêm um acompanhamento constante do desenvolvimento das minhocas em cada célula, e têm uma estimativa extremamente precisa da produtividade de cada uma das células.
Um pesquisador da OBM inventou e construiu uma máquina colhedeira de minhocas, e quer testá-la na fazenda. A máquina tem a largura de uma célula, e em uma passada pelo terreno de uma célula colhe todas as minhocas dessa célula, separando-as, limpando-as e empacotando-as. Ou seja, a máquina eliminará uma das etapas mais intensivas de mão-de-obra no processo de produção de minhocas. A máquina, porém, ainda está em desenvolvimento, e tem duas restrições:
• não se desloca em aclive, de forma que deve movimentar-se ou no mesmo nível, ou em declive.
• a máquina não consegue efetuar a colheita de minhocas da espécie minhocus enroscus. Todas as minhocas dessa espécie colhidas são inutilizadas e, pior, como a máquina enguiça, um número igual de minhocas de outras espécies (já colhidas ou que venham a ser colhidas) é também inutilizado.
O campo de minhocas está em uma área de terreno tal que, na direção Norte - Sul o terreno é em declive (o lado Norte é mais alto, o lado Sul é mais baixo), e totalmente plano na direção Leste-Oeste.
A figura abaixo mostra um mapa da fazenda, mostrando a produtividade estimada de cada uma das células para colheita com a nova máquina. Note que as células onde são criadas minhocas da espécie minhocus enroscus têm produtividade negativa.

Decidiu-se então que seria efetuado um teste com a máquina, tendo como ponto de partida a célula mais ao norte e mais a oeste, e como ponto de chegada a célula mais ao sul e mais a leste. Além disso, deseja-se que a máquina colha o maior número possível de minhocas durante o trajeto. Decidiu-se ainda que a máquina não deve, durante o trajeto, passar mais de uma vez sobre a mesma célula. Note que a máquina pode movimentar-se nas direções N - S, L - O, O - L, mas não pode movimentar-se na direção S - N (morro acima). A figura abaixo ilustra trajetos válidos e não válidos para o teste da máquina.
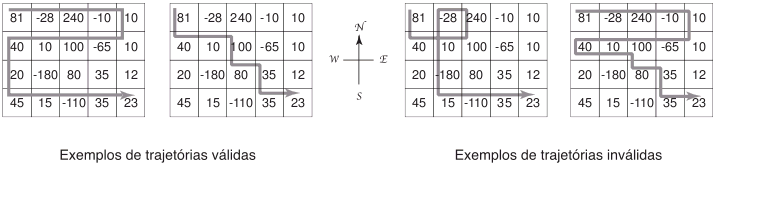
Tarefa
Escreva um programa que, fornecido o mapa do campo de minhocas, descrevendo a produtividade estimada em cada célula, calcule o maior número esperado de minhocas que podem ser colhidas e aproveitadas pela máquina durante o teste, conforme descrito acima.
Entrada
A entrada é composta de vários conjuntos de teste. A primeira linha de um conjunto de teste contém dois números inteiros N e M , representando respectivamente o número de linhas (1 <= N <= 1000) e o número de colunas (1 <= M <= 1000) de células existentes no campo experimental de minhocas. Cada uma das i linhas seguintes (1 <= i <= N) contém M inteiros, representando as produtividades estimadas das células presentes na linha i de celulas do campo de minhocas. Em cada campo da entrada é sempre possível aproveitar alguma minhoca colhida. O final da entrada é indicado por N = M = 0.
Saída
Para cada conjunto de teste da entrada seu programa deve produzir três linhas na saída. A primeira linha deve conter um identificador do conjunto de teste, no formato ‘Teste n’, onde n é numerado seqüencialmente a partir de 1. A segunda linha deve conter um número inteiro indicando o maior número esperado de minhocas que podem ser colhidas e aproveitadas pela máquina durante o teste. A terceira linha deve ser deixada em branco. A grafia mostrada no Exemplo de Saída, abaixo, deve ser seguida rigorosamente.
Exemplo de entradaEntrada: 3 4 81 28 240 10 40 10 100 240 20 180 110 35 4 3 2 -1 7 4 2 -1 -6 -4 1 3 2 3 0 0 Saída: Teste 1 1094 Teste 2 15 |
Restrições
1 <= N <= 1000
1 <= M <= 1000
-500 <= Produtividade de uma célula <= 500
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2008-04-02 |
| Tempo limite: | 0.200s-0.401s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP PERL6 PY_NBC SCALA TCL |
| Origem: | Olimpíada Brasileira de Informática 2005 -- Seletiva 1 |
hide comments
|
2012-07-09 15:37:08 Antonio Carlos de Nazaré Júnior [UFOP/UFMG]
Este problema năo está sendo avaliado pelo juiz, já realizei várias submissőes e todas estăo com o resultado: "aguarde..." |
|
|
2009-09-02 21:46:39 Everton Lima[INF - UFG]
Alguem poderia me dizer qual a complexidade minima pra esse problema? |
