| Submeter | Todas submissőes | Melhores | Voltar |
QUADRA11 - Quadrado aritmético |
Arnaldo e Bernardo são dois garotos que compartilham um peculiar gosto por curiosidades matemáticas. Nos últimos tempos, sua principal diversão tem sido investigar propriedades matemágicas de tabuleiros quadrados preenchidos com inteiros. Um belo dia, Arnaldo desenhou o tabuleiro da seguinte figura.
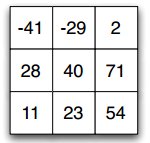
— Olha só, várias somas nesse quadrado são iguais! — exclamou Bernardo.
— Como assim? — devolveu, intrigado, Arnaldo.
— Observe:
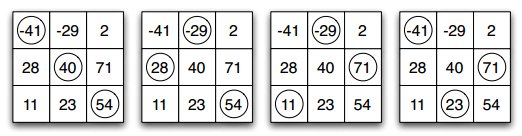
— É mesmo! (−41) + 40 + 54 dá 53, 28 + (−29) + 54 também! — exclamou Arnaldo.
— Eu já verifiquei: existem 6 formas de escolhermos 3 células deste quadrado de forma que cada linha e coluna tenha exatamente uma célula escolhida. Em todas elas, a soma dá 53. Além disso, todos os números são distintos nesse quadrado. — notou Bernardo, exibindo suas habilidades aritméticas.
— Que bacana! Esse quadrado é realmente mágico! Ou, melhor, esse quadrado é realmente aritmético! Será que existem mais quadrados como esse?
Uma escolha legal de células é uma escolha em que toda linha e toda coluna tenha exatamente uma célula escolhida. Um quadrado aritmético de tamanho N e soma S é um tabuleiro de inteiros de N linhas e N colunas em que qualquer escolha legal tem soma S e em que todos os números são distintos.
Sua tarefa, neste problema, é gerar um quadrado aritmético de tamanho N e soma S, dados N e S. Como Arnaldo e Bernardo vão querer conferir a sua solução em suas calculadoras, você não deve gerar um quadrado em que alguma célula tenha valor absoluto maior do que 109.
Entrada
A primeira e única linha da entrada contém dois números inteiros N e S (1 ≤ N ≤ 1000 e −1000 ≤ S ≤ 1000) representando, respectivamente, o tamanho e a soma do quadrado aritmético pedido.
Saída
Seu programa deve imprimir N linhas, cada uma com N inteiros entre −109 e 109, representando o quadrado aritmético pedido. Para uma mesma entrada, podem existir vários quadrados aritméticos válidos; seu programa deve imprimir qualquer um deles, mas apenas um.
É garantido que existirá pelo menos um quadrado aritmético válido para cada entrada testada.
Restrições
- 1 ≤ N ≤ 1000
- −1000 ≤ S ≤ 1000
- −109 ≤ valor de cada célula ≤ 109
Exemplos
Observe que, neste problema, para uma mesma entrada, podem existir várias saídas corretas. As saídas abaixo indicam apenas uma de várias potenciais soluções. Contanto que sua saída seja um quadrado aritmético válido segundo as condições do enunciado, sua solução será considerada correta, mesmo que não seja igual aos exemplos indicados abaixo.
Entrada 2 49 Saída 23 40 9 26 Entrada 3 53 Saída -41 -29 2 28 40 71 11 23 54 Entrada 1 -55 Saída -55
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2012-03-10 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP PERL6 PY_NBC SCALA TCL |
| Origem: | OBI 2011 - fase 1 nível 2 |
hide comments
|
2014-03-05 06:17:22 Marcos Kawakami
Foram inseridos novos casos de teste. Algumas submissőes deixaram de passar. |
|
|
2012-08-20 00:01:06 Ricardo Oliveira [UFPR]
Um código AC está imprimindo a matriz 1 2 2 3 para o caso n=2, s=4, o que năo deveria ser válido. Talvez o juiz esteja fraco? |
