| Submeter | Todas submissőes | Melhores | Voltar |
TAREFMG - Agendamento de tarefas |
A construção de um sistema de software complexo pode ser estruturada como um conjunto de tarefas logicamente relacionadas, como a análise de requisitos, o projeto da arquitetura do sistema, a implementação dos subcomponentes de software que formarão o sistema final, a escrita de documentação, a validação e outras. Algumas dessas tarefas só podem ser executadas depois que outras tarefas das quais elas dependem tenham sido concluídas, mas várias tarefas podem ser executadas em paralelo desde que elas não dependam umas das outras.
Suponha que sejam conhecidas todas as tarefas necessárias e, para cada tarefa, qual o tempo necessário para execução dela e quais são as outras tarefas das quais ela dependa. Suponha também que um número ilimitado de tarefas possam ser executadas em paralelo (desde que todas as dependências de cada uma delas já tenham sido satisfeitas). Uma pergunta óbvia é qual o menor tempo necessário para completar a construção do sistema de software (i.e., executar todas as tarefas). Considere o exemplo da figura abaixo, onde as tarefas são representadas por letras e uma seta de uma tarefa X para uma tarefa Y indica que X depende de Y (os números entre parênteses indicam o número de dias necessários para executar cada tarefa):
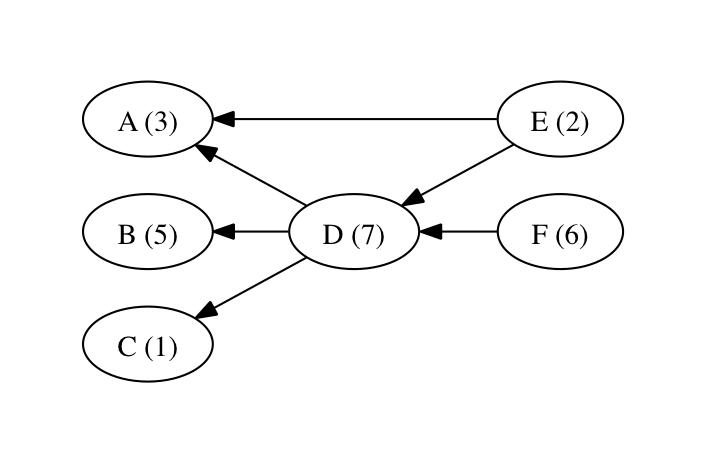
As tarefas A, B e C não possuem nenhuma dependência e podem ser executadas em paralelo. A tarefa D depende dessas três, e as tarefas E e F dependem da tarefa D, então nenhuma outra tarefa pode ser executada até que as tarefas A, B e C sejam concluídas.
Assim, é necessário esperar 5 dias até que a tarefa B esteja concluída. Quando isso ocorrer, as tarefas A e C também já estarão concluídas (porque elas foram executadas em paralelo) e então poderemos executar a tarefa D. Ao fim de mais 7 dias necessários para a conclusão da tarefa D, podemos começar a execução das tarefas E e F. A tarefa E estará concluída em 2 dias, mas a tarefa F levará 6 dias para ficar pronta. Logo, o tempo necessário para a execução de todas as tarefas é de 5+7+6=18 dias.
No exemplo, assumimos que uma tarefa ia ser iniciada tão logo quanto todas as suas dependências estivessem concluídas. Por exemplo, a tarefa A foi iniciada no dia zero e concluída no dia 3, a tarefa D foi iniciada no dia 5 e concluída no dia 12 e a tarefa E (que depende apenas das tarefas A e D) foi iniciada no dia 12 e concluída no dia 14. Porém, nem sempre é necessário iniciar uma tarefa tão logo quanto possível para garantir que o tempo total de execução seja mínimo. Como vimos, o menor tempo de execução para o exemplo dado é de 18 dias. Como a tarefa E leva apenas 2 dias para ser concluída, poderíamos deixar para iniciá-la até o dia 16 sem alterar o prazo total. Da mesma forma, a tarefa A podia ser iniciada até no dia 2, pois ela dura 3 dias e todas as tarefas que dependem dela também dependem direta ou indiretamente da tarefa B, que só será concluída no dia 5. Essa flexibilidade na data de início pode ser interessante por diversos motivos. Por exemplo, se as três tarefas A, B e C forem todas iniciadas no dia 0, então seriam necessárias três equipes diferentes, uma para executar cada tarefa. Porém, se a data de início da tarefa A for adiada para o dia 2, então as três tarefas poderiam ser executadas por apenas duas equipes: uma que executa a tarefa B, e outra que executa primeiro a tarefa C e depois a tarefa A.
Na empresa onde você trabalha, esse agendamento de tarefas é feito de forma manual. Por muito tempo, esse sistema funcionou bem, mas, agora, os projetos de software estão ficando mais complexos, com um número grande de tarefas, de forma que fica impraticável para um gerente realizar esse agendamento manualmente. Devido a isso, seu chefe pediu que você criasse um programa que, dada uma descrição das tarefas, suas durações e suas dependências, determine o prazo mínimo para conclusão de todas essas tarefas e, para cada tarefa, quais são o primeiro e o último dia no qual a tarefa pode ser iniciada de forma tal que seja possível concluir todas elas dentro desse prazo mínimo.
Entrada
Há vários casos de teste.
Cada caso de teste começa com um inteiro N, que representa o número de tarefas (0 < N ≤ 1000). Cada uma das N linhas seguintes descreve uma tarefa, e vem no formato <id> <duracao> <k> <dep 1> <dep 2> ... <dep k>, onde:
- <id> é um inteiro que identifica aquela tarefa (entre 0 e N-1, inclusive; tarefas diferentes possuem identificadores diferentes);
- <duracao> é um inteiro que representa o número de dias necessário para executar aquela tarefa (entre 1 e 100, inclusive);
- <k> é o número de tarefas das quais aquela tarefa depende (entre 0 e N-1, inclusive);
- Os k inteiros <dep i> representam os identificadores das tarefas das quais essa tarefa depende.
Você pode supor que nenhuma tarefa depende dela mesma, nem direta nem indiretamente.
A entrada termina com N = 0, que não deve ser processado.
Saída
Para cada caso de teste, imprima uma linha no formato Prazo: X dias, onde X é o menor número de dias necessário para concluir todas as tarefas. Em seguida, imprima uma linha para cada tarefa, no formato Tarefa #I: min=A, max=B, onde I é o identificador da tarefa, A é o índice do menor dia no qual essa tarefa pode ser iniciada e B é o índice do maior dia no qual essa tarefa pode ser iniciada (os dias são indexados a partir de zero). As tarefas devem ser impressas em ordem crescente de identificador.
Ao fim de cada caso de teste, inclusive o último, imprima uma linha contendo apenas 3 hífens: ---
Exemplos
Entrada: 6 0 3 0 1 5 0 2 1 0 3 7 3 0 1 2 4 2 2 0 3 5 6 1 3 0 Saída: Prazo: 18 dias Tarefa #0: min=0, max=2 Tarefa #1: min=0, max=0 Tarefa #2: min=0, max=4 Tarefa #3: min=5, max=5 Tarefa #4: min=12, max=16 Tarefa #5: min=12, max=12 ---
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2012-06-21 |
| Tempo limite: | 1.466s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP PERL6 PY_NBC SCALA TCL |
| Origem: | Maratona Mineira 2012 |
