| Submeter | Todas submissőes | Melhores | Voltar |
TESOUR11 - Caça ao tesouro |
Capitão Tornado é um pirata muito cruel que faz qualquer coisa por dinheiro. Há alguns dias, o capitão soube da existência de um tesouro numa ilha deserta, e agora tenta determinar sua posição.
A ilha pode ser vista como um quadriculado N × N de terra cuja posição (0, 0) está a sudoeste, a posição (N−1, 0) está a sudeste, a posição (0, N−1) está a noroeste e a posição (N−1, N−1) está a nordeste. Em alguma posição desse quadriculado está o tesouro.
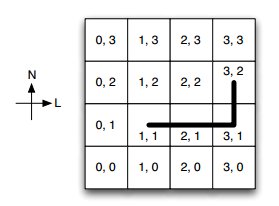
Uma curiosidade importante é a perna de pau que o capitão possui. Ela impede que o capitão se locomova em direções que não a horizontal ou a vertical: para ir da posição (1, 1) para a posição (3, 2), por exemplo, o capitão é obrigado a gastar três passos. É claro que o capitão sempre escolhe, dentro de suas limitações, um caminho com o menor número de passos possível. Chamamos esse modo de andar de passos de capitão. Um exemplo de caminho por passos de capitão entre (1, 1) e (3, 2) é ilustrado na figura a seguir.
Como em toda boa caça ao tesouro, o capitão não conhece a posição onde o tesouro se encontra: ele possui um mapa que corresponde à geografia da ilha. Em algumas posições desse mapa, existem pistas escritas. Cada pista consiste em um número D, que indica a menor distância em passos de capitão entre a posição em que a pista se encontra e a do tesouro.
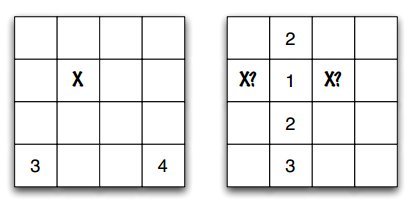
Observe que, dependendo da disposição das pistas, a posição do tesouro pode estar determinada de maneira única ou não. Na figura acima e à esquerda, as duas pistas são suficientes para se saber, com certeza, onde está o tesouro; na figura à direita, as quatro pistas dadas ainda possibilitam que tanto a posição (0, 2) quanto a (2, 2) guardem o tesouro. Nesse último caso, não se pode determinar, com certeza, qual é a localização do tesouro.
Dadas as pistas que o capitão possui, sua tarefa é determinar se as pistas fornecem a localização exata do tesouro e, caso positivo, qual ela é.
Entrada
A primeira linha contém dois inteiros positivos N e K, onde N é a dimensão do quadriculado e K é o número de pistas no mapa que o capitão possui.
Cada uma das próximas K linhas contêm três inteiros X, Y e D, informando que existe uma pista na posição (X, Y) contendo o número D. Essa pista indica que o tesouro encontra-se a D passos de capitão da posição da pista.
É garantido que, com essas pistas, existe ao menos uma localização possível para o tesouro. Além disso, o mapa não contém duas pistas na mesma posição.
Saída
Se as pistas forem suficientes para determinar com certeza a localização do tesouro, seu programa deve imprimir uma única linha com dois inteiros, X e Y , indicando que o tesouro encontra-se na posição (X, Y).
Caso contrário, seu programa deve imprimir uma única linha com dois inteiros iguais a −1, como nos exemplos de saída a seguir.
Restrições
- 2 ≤ N ≤ 100
- 1 ≤ K ≤ 100
Exemplos
Entrada 4 2 0 0 3 3 0 4 Saída 1 2 Entrada 4 4 1 0 3 1 1 2 1 2 1 1 3 2 Saída -1 -1 Entrada 3 3 0 0 2 1 1 2 2 0 4 Saída 0 2
| Adicionado por: | Wanderley Guimarăes |
| Data: | 2012-03-10 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP PERL6 PY_NBC SCALA TCL |
| Origem: | OBI 2011 - fase 1 nível 2 |
hide comments
|
2016-04-08 00:33:07 Elsio [UFABC]
Tem um outro problema com o mesmo nome. http://br.spoj.com/problems/TESOURO/ Se for uma lista de exercícios peça pra o professor especificar |
