| Submeter | Todas submissőes | Melhores | Voltar |
|
Problem hidden
TOUGH - Bits. Exponents and Gcd |
Rastas's has been given a number n. Being weak at mathematics, she has to consider all the numbers from 1 to 2n - 1 so as to become perfect in calculations. (You can assume each number is consider as a soldier).
We define the strength of number i as the number of set bits (bits equal to 1) in binary representation of number i.
If the greatest common divisor of numbers a and b is gcd(a, b),
Rastas would like to calculate the function S which is equal to: 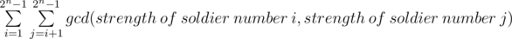
As the friend of Rastas, it's your duty to calculate S modulo 109 + 7.
Input
The first line of the input contains the number of test cases, T. Each of the next T lines contains an integer n, as mentioned in the question.
Output
For each value of n given, find the value of the function S.
Constraints
Sum of n over all test cases doesn't exceed 2500.
Example
Input: 3 1 2 5 Output: 0 3 680
| Adicionado por: | likecs |
| Data: | 2016-02-05 |
| Tempo limite: | 1s |
| Tamanho do fonte: | 10000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Linguagem permitida: | Todas exceto: ASM64 CLOJURE ERL FSHARP GOSU JS-MONKEY PERL6 PY_NBC SCALA TCL |
| Origem: | Own problem |
