| Submit | All submissions | Best solutions | Back to list |
AE00 - Rectangles |
Byteman has a collection of N squares with side 1. How many different rectangles can he form using these squares?
Two rectangles are considered different if none of them can be rotated and moved to obtain the second one. During rectangle construction, Byteman can neither deform the squares nor put any squares upon any other ones.
Input
The first and only line of the standard input contains one integer N (1 <= N <= 10000).
Output
The first and only line of the standard output should contain a single integer equal to the number of different rectangles that Byteman can form using his squares.
Example
For the input data:
6
the correct result is:
8
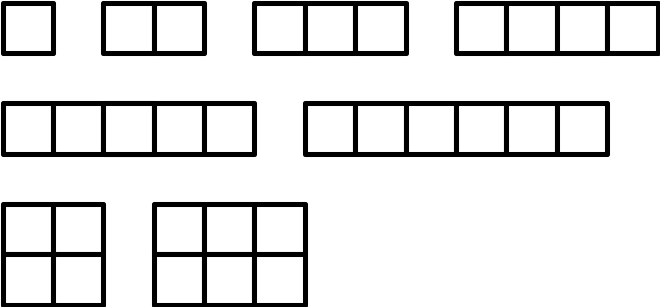
Task author: Jakub Radoszewski.
| Added by: | Race with time |
| Date: | 2009-05-03 |
| Time limit: | 1s |
| Source limit: | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Languages: | All except: ERL JS-RHINO NODEJS PERL6 VB.NET |
| Resource: | Algorithmic Engagements 2009 |
hide comments
|
||||||||||||||
|
2019-10-25 03:53:18
AC in one go! |
||||||||||||||
|
2019-09-14 14:16:41
AC in one go :D |
||||||||||||||
|
2019-08-09 09:07:30
O(sqrt(n)) with a quite straighfoward solution using the picture provided. |
||||||||||||||
|
2019-07-30 12:09:37
AC,Hint:find factors. Last edit: 2019-07-30 12:12:14 |
||||||||||||||
|
2019-07-19 13:59:52
AC in one go! |
||||||||||||||
|
2019-06-02 11:26:24
AC in one go. O(n*log(n)) solution. Last edit: 2019-06-02 11:28:18 |
||||||||||||||
|
2019-04-11 16:59:34
did it in O(n*sqrt(n))... =( |
||||||||||||||
|
2019-04-04 13:15:10
See also https://oeis.org/A094820 They also have an implementation there which does it in O(sqrt(n)), so I guess faster will not be possible (otherwise they'd state the algorithm there). Last edit: 2019-04-04 13:19:05 |
||||||||||||||
|
2019-03-22 06:51:49
AC in 2 go ! haha @sqrt(n) |
||||||||||||||
|
2019-03-20 16:45:20
for(int i=1;i<=sqrt(n);i++) { sum+=n/i - i + 1; } |
||||||||||||||


 RSS
RSS